Venerdì scorso abbiamo fatto il seminario sulla valutazione dell’insegnamento. C’era un po’ meno della metà degli studenti, in 94 hanno compilato i moduli per la valutazione del corso.
Un dato che, a fare le cose sul serio, dovrebbe essere sconfortante ma che invece va preso con soddisfazione visto le condizioni letargiche nelle quali versano gli atenei.
Su questo non ho molto altro da dire che non abbia già detto. Voglio invece aggiungere qualcosa al seminario che avevo “nascosto” nel precedente e che si potrebbe intitolare
Seguiamo le orme del caos
L’idea mi era venuta ripensando ad alcune delle tante e piacevoli discussioni fatte nel corso del semestre. Gli spunti erano due:
- Mi sembrava utile tornare ad approfondire nei limiti del possibile l’idea che un sistema possa produrre qualcosa di superiore alla mera somma delle sue parti e quindi che l’approccio riduzionista di studiare le parti per dedurne l’insieme possa essere utile ma insufficiente, specialmente nel caso dei sistemi complessi. Che è come dire quasi tutto. Poiché questo concetto è strettamente legato alla nozione di caos che è molto più vicina a noi, ubiquitaria e molto meno “caotica” di quanto si possa pensare, ho provato a farne una semplice introduzione. Mi sono servito dell’equazione logistica che nasce dalla necessità di vedere come evolve una popolazione di creature in un ambiente dalle risorse limitate. Abbiamo fatto un po’ di conti alla lavagna utilizzando la matematica che si studia nei primi anni del liceo per rendersi conto che il caos è proprio lì, dietro l’angolo, indissolubilmente e mirabilmente intrecciato con l’ordine. Lo scopo era di mostrare che se non si tiene ugualmente conto di questa duplice faccia della Natura, la nostra speranza di capire qualcosa dei sistemi vitali è vana.
- Inoltre volevo precisare meglio la critica ai programmi scolastici laddove sostengo che non danno un’idea corretta della conoscenza dell’uomo del XX secolo (non ho sbagliato, non del XXI ma nemmeno del XX). In pratica sostengo che la scuola, nel suo insieme, contribuisce molto poco a quello che in taluni, troppo pochi, un giorno diverrà un atteggiamento della vita che potremmo chiamare, forse, cultura. Tutto questo al netto di alcune donne e uomini eccezionali che nella scuola fanno un lavoro straordinario. Tante donne e tanti uomini che nella massa di un sistema sono pur sempre delle eccezioni. La precisazione che volevo fare concerneva il fatto che non è questione di aggiungere ennesime materie, tipo relatività o fisica quantistica. Giustamente alcuni studenti ipotizzavano che sarebbero state materie troppo difficili. Certo, e aggiungo io ennesime scatole chiuse. Si potrebbe arricchire la vita scolastica con queste straordinarie visioni ma non per la via delle materie. Prima, c’è da rivedere il modo di strutturare l’organizzazione dell’insegnamento che in realtà deriva dal modo di concepire la conoscenza stessa del mondo. Ed allora, per dare un’idea di questo ho cercato di portare gli studenti sulle orme del caos con la testa ben alta, non perdendo mai occasione di cogliere i nessi con varie discipline.
Appena avrò sistemato il materiale rinfrescherò questo post con link alle versioni audio e video di questo seminario.
Qui vorrei aggiungere alcune suggestioni che avevo omesso al volo per non appesantire il discorso poiché a fine semestre mi pare di vedere che questi ragazzi non ne possano proprio più di lezioni!
Orbene, per introdurre la mappa logistica abbiamo preso le mosse dal caso di una popolazione che si moltiplica senza vincoli alcuni, dai conigli di Fibonacci. Abbiamo accennato a come la serie di Fibonacci che descrive questo fenomeno sia al limite di natura esponenziale e come la esponenzialità sia un concetto ubiquitario nelle scienze, da quelle fisiche a quelle sociali.
Abbiamo messo in luce come in questo contesto l’esponenzialità sia legata al concetto di linearità che si esprime in un ritmo di crescita di una popolazione che è costante e non dipende da niente altro. Il ritmo di crescità è costante e da questo segue la crescita esponenziale.
L’esponenzialità porta all’esplosione e quindi in natura può essere utilizzata in modo molto limitato per descrivere i fenomeni. Un fatto che l’economia fa ancora fatica a digerire.
È utile avere presente la potenza devastante dell’esplosione esponenziale ed allora vi suggerisco di leggere questa paginetta delle dispense dove, prendendo le mosse da quante cose si possono contare con una serie di bit e passando, grazie a due terzine di Dante Alighieri, per la novella indiana del re, del matematico e degli scacchi, si appura che raddoppiando i chicchi di grano per ognuna delle 64 caselle di una scacchiera si ottengono 10 miliardi di mililardi di chicchi e che tale quantità equivale al fabbisogno di grano dell’Italia per 10000 anni.
Incidentalmente, nel seminario avevamo notato che 10 miliardi di milardi è il numero delle molecole d’acqua in una delle nostre cellule, unità fondamentale della vita delle creature complesse. In ogni cellula 10 miliardi di miliardi di molecole che sbattendo caoticamente l’una contro l’altra favoriscono gli incontri casuali fra gli altri miliardi di miliardi di molecole strutturali di ogni tipo per alimentare la rete di reazioni biochimiche nel processo globale che è poi la vita della cellula medesima. Il moto caotico di questa miriade di molecole alimenta la vita. Il caos è il motore della vita.
Poi siamo tornati alla crescita di una qualsiasi popolazione introducendo un limite costituito dalle risorse disponibili. Ed è così venuta fuori l’equazione logistica. Essa nasce dall’ammissione che il ritmo di crescita dipenda anche dalle risorse e, quindi anche dalla popolazione esistente: se è vicina alla saturazione delle risorse cresce poco o nulla, se è scarsa cresce come se non vi fossero limiti. Abbiamo commentato come questa dipendenza non lineare del ritmo di crescita coinvolga un meccanismo di feedback del sistema e come le reti, di ogni genere si nutrano e vivano di feedback multipli.
Avevo previsto di giocare nel seminario con l’equazione logistica in una sorta di laboratorio del caos ma dall’aula non è stato possibile accedere al sito che ci serviva 😦 ed abbiamo fatto con la lavagna.
Chi vuole può recuperare la suggestione qui: questa è una descrizione dell’equazione logistica e questo il laboratorio. In quest’ultimo, provate a seguire l’evoluzione della popolazione con i valori per r uguali a 1.45, 2.75, 3.2, 3.5, 4; per il valore iniziale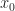 
usate 0.1 e usate numeri di iterazioni N fra 20 e 100 per vedere che succede.
Questo semplice esperimento matematico serve ad esplorare quei punti magici nei quali la natura si affida al caso per passare da una certa configurazione di un sistema ad un’altra. Sono punti di biforcazione nei quali un sistema può dare vita all’emergenza di un fenomeno del tutto nuovo del quale nelle sue parti non v’è traccia alcuna.
Nel seminario avevamo messo in relazione questo concetto con l’intuizione di Giacomo Leopardi che abbiamo fatto risuonare in aula recitando le sue parole:
Scomponete una macchina complicatissima, toglietele una gran parte delle sue ruote, e ponetele da parte senza pensarvi più; quindi, ricomponete la macchina, e mettetevi a ragionare sopra le sue proprietà, i suoi mezzi, i suoi effetti: tutti i vostri ragionamenti saranno falsi, la macchina non è più quella, gli effetti non sono quelli che dovrebbero, i mezzi sono indeboliti, cambiati, o fatti inutili; voi andate arzigogolando sopra questo composto, vi sforzate di spiegare gli effetti della macchina dimezzata, come s’ella fosse intera; speculate minutamente tutte le ruote che ancora lo compongono, ed attribuite a questa o quella un effetto che la macchina non produce più, e che le avevate veduto produrre in virtù delle ruote che le avete tolte ecc. ecc. Così accade nel sistema della natura, quando l’è stato tolto e staccato di netto il meccanismo del bello, ch’era congegnato e immedesimato con tutte le altre parti del sistema, e con ciascuna di esse. (4 Ottobre 1821, Zibaldone di pensieri, pagina 1837)
Stamani ho ritrovato lo stesso concetto in un brano del fumetto (in realtà è un libro) Watchmen di Alan Moore, nell’incipit dell’appendice al volume VII, concetto che qui si collega anche alla nostra metafora della passeggiata nel bosco:
Is it possible, I wonder, to study a bird so closely, to observe and catalogue its peculiarities in such minute detail, that it becomes invisible? Is it possible that while fastidiously calibrating the span of its wings or the length of its tarsus, we somehow lose sight of its poetry? That in our pedestrian descriptions of a marbled or vermiculated plumage we forfeit a glimpse of living canvases, cascades of carefully toned browns and golds that would shame Kandisnsky, misty explosions of color to rival Monet? I believe that we do. I believe that in approaching our subject with the sensibilities of statisticians and dissectionists, we distance ourselves increasingly from the marvelous and spell-binding planet of imagination whose gravity drew us to our studies in the first place.
This is not to say that we should cease to establish facts and to verify our information, but merely to suggest that unless those facts can be imbued with the flash of poetic insight then they remain dull gemms; semi-precious stones scarcely worth collecting.
Il bello di cui scrive Leopardi deriva dalla percezione dell’emergenza del nuovo, che oggi sappiamo essere un meccanismo fondamentale della Natura.
La sterilità di tanto insegnamento scolastico deriva, in buona parte ed escluse le eccezioni, dall’assenza di visione immaginifica e poetica dei fatti scentifici e dall’astrazione degli insegnamenti umanistici dal resto del mondo.
Ne approfitto per commentare la bella citazione dello psicologo Howard Gardner riportata sulla locandina …
Andreas Formiconi 